Step-by-step explanation:
It looks like you're trying to make the coherent statement ...
The average rate of change over the interval [a, x] is ...

The limit ...
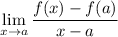
is the slope of the line. It is also the limit of the average rate of change, which is the instantaneous rate of change at x=a.