Question

An investigator compares the durability of two different compounds used in the manufacture of a certain automobile brake lining. A sample of 243 brakes using Compound 1 yields an average brake life of 37,866 miles. A sample of 268 brakes using Compound 2 yields an average brake life of 45,789 miles. Assume that the population standard deviation for Compound 1 is 4414 miles, while the population standard deviation for Compound 2 is 2368 miles. Determine the 95% confidence interval for the true difference between average lifetimes for brakes using Compound 1 and brakes using Compound 2.

Answer 1

THEREFORE THE CONFIDENCE INTERVAL from the Z table = ±1.645

Explanation:

Confidence level = 95% = 0.95

compound 1

Number of samples ( n1 ) = 243

Average brake life ( x1 ) = 37866 miles

standard deviation ( ∝ ) = 4414 miles

compound 2

number of samples ( n2 ) = 268

Average brake life ( x2 ) = 45789 miles

standard deviation ( ∝ ) = 2368 miles

Determine the 95% confidence interval for the true difference between average lifetimes

significance level (β) = 1 - confidence level = 1 - 0.95 = 0.05

standard error =
`\sqrt{(\alpha1^2 )/(n1) + (\alpha2^2)/(n2) }` =
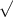`\sqrt{}`( 4414^2/243) + (2368^2/268) =

critical value = 0.05/2 =Z 0.025 = 1.645

THEREFORE THE CRITICAL VALE from the Z table = ±1.645