Due to crime rates in a certain city, home values began to decrease by 4% each year. If a home was purchased in 2015 for $315,000, write and use an exponential function to deter…

Question

asked Nov 2, 2021 201k views

2 Answers

Kokovin Vladislav · Answer 1 · 2021-11-08T12:26:32+0000

Answer:

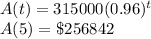
$A(t)=315000(0.96)^t\\A(5)=\$256842$

Explanation:

The exponential function for depreciation is given as:

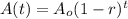A(t)=A_o(1-r)^t where:

$A_o$ is the initial value\\r is the depreciation rate\\t is the number of time period (in years) after the initial point$

In the case of the home:

$A_o=$315,000\\r=4\%=0.04$

Therefore, the exponential function modeling the depreciation of the home's value is:

$A(t)=315000(1-0.04)^t\\A(t)=315000(0.96)^t\\$

We want to determine the worth of the home in 2020.

t=2020-2015=5 years

Therefore:

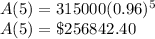
$A(5)=315000(0.96)^5\\A(5)=\$256842.40$

The home is worth $256,842 in the year 2020.