Question

A 5.00-V battery charges the parallel plates in a capacitor, with a plate area of 865 mm2 and an air-filled separation of 3.00 mm. They are then disconnected from the battery and pulled apart (without discharge) an additional 3.00 mm. Neglecting fringing, how much work is required to separate the plates

Answer 1

W = 3.21x10⁻¹¹ J

Step-by-step explanation:

The work required to separate the plates can be calculated using the following equation:

`W = U_(2) - U_(1) = (1)/(2)(C_(2)V_(2)^(2) - C_(1)V_(1)^(2))`

Where:

U₂: is the final stored energy

U₁: is the initial stored energy

C₂: is the final capacitance

C₁: is the initial capacitance

V₁: is the initial potential difference = 5.00 V

V₂: is the final potential difference

The initial and final capacitance is:

`C_(1) = \epsilon_(0)*(A)/(d_(1))`

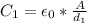
Where:

ε₀: is the vacuum permittivity = 8.85x10⁻¹² C²/(N*m²)

d: is the initial distance = 3.00 mm = 3.00x10⁻³ m

A: is the plate area = 865 mm² = 8.65x10⁻⁴ m²

`C_(1) = \epsilon_(0)*(A)/(d_(1)) = 8.85 \cdot 10^(-12) C^(2)/(N*m^(2))*(8.65 \cdot 10^(-4) m^(2))/(3.00 \cdot 10^(-3) m) = 2.55 \cdot 10^(-12) F`

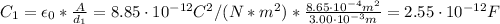
Similarly, C₂ is:

`C_(2) = \epsilon_(0)*(A)/(d_(2)) = 8.85 \cdot 10^(-12) C^(2)/(N*m^(2))*(8.65 \cdot 10^(-4) m^(2))/(3.00 + 3.00 \cdot 10^(-3) m) = 1.28 \cdot 10^(-12) F`

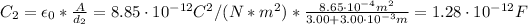
Now, V₂ can be calculated by finding the initial charge (q₁):

`q_(1) = C_(1)V_(1) = 2.55 \cdot 10^(-12) F*5.00 V = 1.28 \cdot 10^(-11) C`

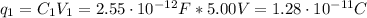
Since, q₁ is equal to q₂, V₂ is:

`V_(2) = (q_(2))/(C_(2)) = (1.28 \cdot 10^(-11) C)/(1.28 \cdot 10^(-12) F) = 10 V`

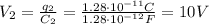
Finally, we can find the work:

`W = (1)/(2)(C_(2)V_(2)^(2) - C_(1)V_(1)^(2)) = (1)/(2)(1.28 \cdot 10^(-12) F*(10 V)^(2) - 2.55 \cdot 10^(-12) F(5.00 V)^(2)) = 3.21 \cdot 10^(-11) J`

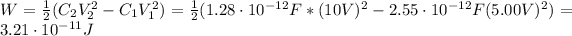
Therefore, the work required to separate the plates is 3.21x10⁻¹¹ J.

I hope it helps you!