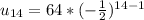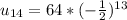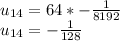Answer:

Explanation:
1) Identify the type of sequence this is; whether it is geometric progression, quadratic sequence or linear sequence.
= Geometric progression
2) Find the
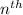 term of this sequence. Every sequence of geometric progression is written in
term of this sequence. Every sequence of geometric progression is written in
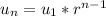 form, where
form, where
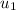 is the first term of the sequence and
is the first term of the sequence and
 is the common ratio. To find the
is the common ratio. To find the
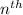 term of this sequence, we need to find the common ratio (
term of this sequence, we need to find the common ratio (
 ) first.
) first.
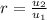
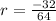
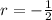
2.1) Write it in
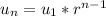 form.
form.
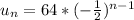
3) Find the
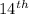 term by substituting 14 into the
term by substituting 14 into the
 's.
's.