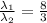Answer:
The ration of the two wavelength is
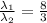
Step-by-step explanation:
Generally two slit constructive interference can be mathematically represented as
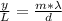
Where y is the distance between fringe
d is the distance between the two slit
L is the distance between the slit and the wall
m is the order of the fringe
given that y , L , d are constant we have that

So
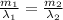
So
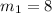
and
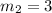
=>
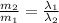
=>
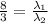
So