Question

a paraellel plate capacitor consists of 2 large circular sheets of metal separated by 1.53 cm. The electric field energy density betwwen plates is 4.41 J/m3 while the capacitor holds .127 J of potential energy. What is the radius of the circular platyes?

Answer 1

The radius of the circular plate is 0.774 m

Step-by-step explanation:

Given;

distance between the parallel plates, d = 1.53 cm = 0.0153 m

electric field energy density between plates,
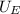`U_E` = 4.41 J/m³

Potential energy of the capacitor,
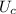`U_c` = 0.127 J

Energy density is given as;

`U_E = (U_c)/(V)`

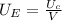
where;

V is volume

`V = (U_c)/(U_E) = (0.127)/(4.41) = 0.0288 \ m^3`

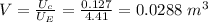
Volume is given as;

V = Ad

where;

A is area

A = V / d

A = (0.0288) / (0.0153)

A = 1.882 m²

Area of circular plate is given as;

A = πr²

where;

r is the radius of the circular plate

`r = \sqrt{(A)/(\pi) } \\\\r = \sqrt{(1.882)/(\pi)}\\\\r = 0.774 \ m`

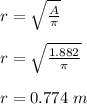
Therefore, the radius of the circular plate is 0.774 m