Question

1. Given the following information about a hypothesis test of comparing the two variances based on independent random samples, what is the critical value of the test statistic at a significance level of .05? Assume that the samples are obtained from normally distributed populations having equal variances.

H0: A = B
H1: A > B
X ¯ 1 = 12
X ¯ 2 = 9
s1 = 4
s2 = 2
n1 = 13
n2 = 10
A. Reject H0 if Z > 1.96
B. Reject H0 if Z > 1.645
C. Reject H0 if t > 2.08
D. Reject H0 if t > 1.782
E. Reject H0 if t > 1.721
2. Given the following information about a hypothesis test of the difference between two means based on independent random samples, what is the standard deviation of the difference between the two means? Assume that the samples are obtained from normally distributed populations having equal variances.
H0: A = B
H1: A > B
X ¯ 1 = 12
X ¯ 2 = 9
s1= 5
s2 = 3
n1 =13
n2 =10
A. 1.792
B. 1.679
C. 2.823
D. 3.210
E. 1.478

Answer 1

1. E. Reject H0 if t > 1.721

2. B. 1.679

Explanation:

This would be a hypothesis test for the difference between two means. In the way that the alternative hypothesis.

The critical value depends on the significance level, the test type (one-tail or two-tailed) and the degrees of freedom.

This is a t-test type, so the statistic is t and not z. In the way that the alternative hypothesis, where only matter if the mean A is significantly bigger than mean B, this is a one-tail test.

The degrees of freedom can be calculated as:

`df=n_1+n_2-2=13+10-2=21`

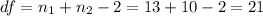
Then, for a one-tail t-test, with significance level of 0.05 and 21 degrees of freedom, the critical value is t=1.721.

The standard deviation of the difference between the two means can be calculated as:

`s_(M_d)=\sqrt{(\sigma_1^2)/(n_1)+(\sigma_2^2)/(n_2)}=\sqrt{(5^2)/(13)+(3^2)/(10)}\\\\\\s_(M_d)=√(1.923+0.9)=√(2.823)=1.6802`