Question

Tyler flies a plane against a headwind for 4320 miles. The return trip with the wind took 12 hours less time. If the wind speed is 6 mph, how fast does Tyler fly the plane when there is no wind?

Answer 1

The plane travels at a speed of 66 miles per hour without wind.

Explanation:

Tyler trip has to stage, the first one where he went against the wind and the second where he returned with the wind. We know that the wind speed is 6 mph, if we attribute the variable "x" to the speed of the plane without wind, then on the first stage of its trip the total speed relative to the ground was "x - 6", while on the return trip it was "x + 6". We also know that the distance between the trips was the same 4320 miles, but the second stage was 12 hours faster. We will use the average speed formula to solve this problem, this is shown below:

`\text{speed} = \frac{\text{distance}}{\text{time}}`

For the first trip the speed was:

`x - 6 = \frac{4320}{\text{time}_1}\\\\\text{time}_1 = (4320)/(x - 6)`

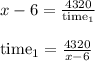
For the second trip the speed was:

`x + 6 = \frac{4320}{\text{time}_2}\\\\\text{time}_2 = (4320)/(x + 6)`

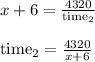
Since the time for the second trip was 12 hours less, then if we add 12 to the second equation it should be equal to the first, so:

`time_2 + 12 = time_1`

`(4320)/(x + 6) +12 = (4320)/(x - 6)\\(4320)/(x+ 6) - (4320)/(x - 6) = -12\\(4320*(x - 6) - 4320*(x + 6))/(x^2 - 36) = -12\\4320*x - 25920 - 4320*x - 25920 = -12*x^2+ 432\\-51840 = -12*x^2 +432\\12*x^2 =51840 + 432\\x^2 = (52272)/(12)\\x^2 = 4356\\x = 66`

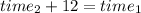
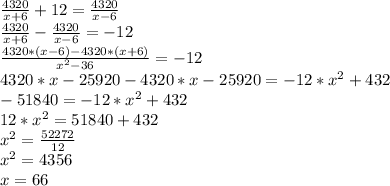
The plane travels at a speed of 66 miles per hour.