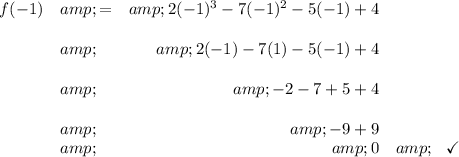well, the remainder theorem says that if the polynomial f(x) has a factor of (x-a), then if we just plug in the "a" in f(x) it'll gives a remainder, assuming (x-a) is indeed a factor, then that remainder must be 0, so if f(a) = 0 then indeed (x-a) is a factor of f(x). After all that mumble jumble, let's proceed, we have (x+1), that means [ x - (-1) ], so if we plug in -1 in f(x), we should get 0, or f(-1) = 0, let's see if that's true.