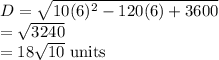Answer:
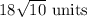
Explanation:
We are given the equation of the line y=3x and a point, say Q(60,0) outside of that line.
We want to find the point on the line y=3x which is closest to Q.
Let P(x,y) be the desired point. Since it is on the line y=3x, it must satisfy the line.
If x=a, y=3a, so the point P has the coordinates (a,3a).
Distance between point Q and P
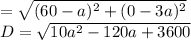
To minimize D, we find its derivative
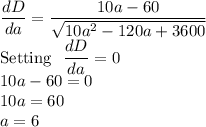
Therefore, the y-coordinate for P is 3*6=18.
The point P=(6,18).
Next, we calculate the distance between P(6,18) and (60,0).