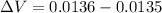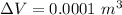Question

The coefficient of linear expansion of copper is 17 × 10-6 K-1. A block of copper 30 cm wide, 45 cm long, and 10 cm thick is heated from 0°C to 100°C What is the change in the volume of the block?

Answer 1

The change in volume is
`\Delta V = 0.0001 \ m^3`

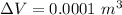
Step-by-step explanation:

From the question we are told that

The coefficient of linear expansion is
`\alpha = 17 *10^(-6) \ K^(-1)`

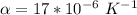
The width of the block is
`b = 30 \ cm = 0.3 \ m`

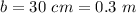
The length is
`l = 45 \ cm = 0.45 \ m`

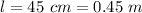
The thickness is
`h = 10 \ cm = 0.1 \ m`

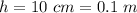
The initial temperature is
`T_1 = 0^oC`

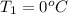
The final temperature is
`T_f = 100 ^oC`

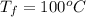
The initial volume is mathematically represented as

`V = l*b*h`

substituting values

`V = 0.30 * 0.45 * 0.10`

`V = 0.0135 \ m^3`

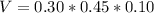
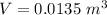
Generally the expansion equation is mathematically represented as

`l' = l (1 + \alpha \Delta T)`

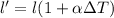
where
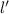`l'` is the new length

substituting values

`l' = 0.45 (1 + 17*10^(-6) * (100-0))`

`l' = 0.4508 \ m`

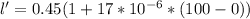
The new width is evaluated as

`b' = b(1 + \alpha \Delta T )`

substituting values

`b'=0.30 ( 1 + 17*10^(-6) * (100 - 0))`

`b'= 0.3005 \ m`

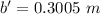
The new thickness is

`h' = h(1 + \alpha \Delta T )`

substituting values

`h' = 0.10 (1 + (17*10^(-6)) (100 - 0) )`

`h' = 0.1001 \ m`

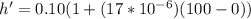
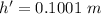
The new volume is mathematically evaluated as

`V' = l'*b'* h'`

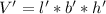
substituting values

`V' = 0.4508 * 0.3005 * 0.1001`

`V' = 0.0136`

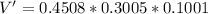
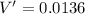
Therefore

`\Delta V = 0.0136 - 0.0135`

`\Delta V = 0.0001 \ m^3`