Question

A 580-turn solenoid is 18 cm long. The current in it is 36 A. A straight wire cuts through the center of the solenoid, along a 2.0-cm diameter. This wire carries a 27-A current downward (and is connected by other wires that don't concern us). What is the magnitude of the force on this wire assuming the solenoid's field points due east?

Answer 1

Answer: The magnitude of the force is 0.079N

Explanation: Please see the attachments below

Answer 2

F = 0.078N

Step-by-step explanation:

In order to calculate the magnitude of the force on the wire you first calculate the magnitude of the magnetic field generated by the solenoid, by using the following formula:

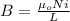`B=(\mu_oNi)/(L)` (1)

μo: magnetic permeability of vacuum = 4π*10^-7 T/A

N: turns of the solenoid = 580

i: current in the solenoid = 36A

L: length of the solenoid = 18cm = 0.18m

You replace the values of all parameters in the equation (1):

`B=((4\pi*10^(-7)T/A)(580)(36A))/(0.18m)=0.145T`

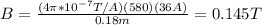
Next, you calculate the force exerted on the wire, by using the following formula:

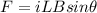`F=iLBsin\theta` (2)

i: current in the wire = 27A

L: length of the wire that perceives the magnetic field (the same as the radius of the solenoid) = 2.0 cm = 0.02m

θ: angle between wire and the direction of B

B: magneitc field in the solenoid = 0.145T

The direction of the wire are perpendicular to the direction of the magnetic field, hence, the angle is 90°.

You replace the values of the parameters in the equation (2):

`F=(27A)(0.02m)(0.145T)sin90\°=0.078N`

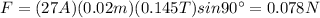
The magnitude of the force on the wire is 0.078N