Question

Rotational dynamics about a fixed axis: A person pushes on a small doorknob with a force of 5.00 N perpendicular to the surface of the door. The doorknob is located 0.800 m from axis of the frictionless hinges of the door. The door begins to rotate with an angular acceleration of 2.00 rad/s2. What is the moment of inertia of the door about the hinges

Answer 1

I = 2 kgm^2

Step-by-step explanation:

In order to calculate the moment of inertia of the door, about the hinges, you use the following formula:

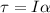`\tau=I\alpha` (1)

I: moment of inertia of the door

α: angular acceleration of the door = 2.00 rad/s^2

τ: torque exerted on the door

You can calculate the torque by using the information about the Force exerted on the door, and the distance to the hinges. You use the following formula:

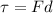`\tau=Fd` (2)

F: force = 5.00 N

d: distance to the hinges = 0.800 m

You replace the equation (2) into the equation (1), and you solve for α:

`Fd=I\alpha\\\\I=(Fd)/(\alpha)`

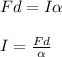
Finally, you replace the values of all parameters in the previous equation for I:

`I=((5.00N)(0.800m))/(2.00rad/s^2)=2kgm^2`

The moment of inertia of the door around the hinges is 2 kgm^2