Question

Data kept by the human resources department of a manufacturing company indicates that t hours after beginning work, the production P (in units completed) of an average worker changes at the rate of P ' ( t ) = 0.1 ( t + 2 ) √ t 2 + 4 t If 2 hours after beginning work, an average worker can complete 14 . Round all answers to 2 decimal places. a . Specify the function that describes the number of units an average worker can complete in terms of the number of hours after beginning work. P ( t ) = b . Find the number of units an average worker can complete 2 hours after beginning work. units c . Approximate the number of units an average worker can complete from hour 4 to hour 5 . about units

Answer 1

a)
`P(t)=0.1\,√(t^2+4t) +13.65`

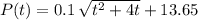
b) P(2) = 14 units

c) from hour 4 to hour 5, an average worker can complete about 0.1 of a unit.

Explanation:

Notice that the problem gives the derivative of the production function, and also an extra piece of information (P(2) = 14) - also called initial condition - that allows us to find the actual production with any additional constant.

Let's work on the "antiderivative" of the function:

`P'(t)= (0.1\,(t+2))/(√(t^2+4t) )`

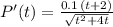
Using the change of variables
`u=√(t^2+4t)` ,
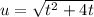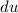`du` becomes
`(1)/(2)(\,2\,(t+2))/(√(t^2+4t) )`

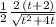
Then, the family of antiderivatives becomes:

`P(t)=0.1\,√(t^2+4t) +C`

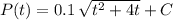
We should be able to determine the constant C using the initial condition for the problem:
`P(2)=14`

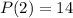
Then we evaluate:

`P(2)=0.1\,√(2^2+4*2) +C\\14=0.1\,√(12) +C\\C=14-0.1\,√(12) \\C=14-0.35\\C=13.65`

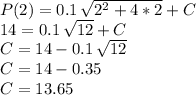
Then the function requested in point a) is:

`P(t)=0.1\,√(t^2+4t) +13.65`

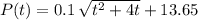
Point b) "Find the number of units an average worker can complete 2 hours after beginning work" was already given as the initial condition, so P(2) = 14 units.

Point c) asks for the number of units an average worker can complete from hour 4 to hour 5, so we calculate the difference:

`P(5)-P(4)=14.32 - 14.22= 0.10\,\, units`

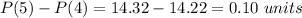
So the average worker can complete one tenths of a unit between hour 4 and hour 5.