Answer:
Area of ΔEDF = 4.5 in²
Explanation:
In the figure attached,
ΔBAC ~ ΔEDF
Property of similarity,
" If two triangles are similar then their corresponding angles will measure the same."
Scale factor for ΔBAC to ΔEDF =
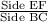
=

"Ratio of the area of similar triangles = Square of the ratio of their corresponding sides"
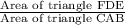 =
=
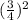
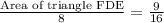
Area of ΔEDF =
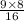
= 4.5 square inches
Therefore, area of ΔEDF = 4.5 in²