Question

A consumer group was interested in comparing the operating time of cordless toothbrushes manufactured by two different companies. Group members took a random sample of 18 toothbrushes from Company A and 15 from Company B. Each was charged overnight and the number of hours of use before needing to be recharged was recorded. Company A toothbrushes operated for an average of 119.7 hours with a standard deviation of 1.74 hours; Company B toothbrushes operated for an average of 120.6 hours with a standard deviation of 1.72 hours. The 90% confidence interval is (-1.93, 0.13). The correct interpretation is:__________

A. We are 90% confident that, on average, there is no difference in operating hours between toothbrushes from Company A compared to those from Company B.
B. We are 90% confident that, on average, there is a difference in operating hours between toothbrushes from Company A compared to those from Company B.
C. We are 90% confident that, on average, the toothbrushes from Company B operate longer before needing to be recharged than the toothbrushes from Company A.
D. We are 90% confident that, on average, the toothbrushes from Company A operate longer before needing to be recharged than the toothbrushes from Company B.

Answer 1

The degrees of freedom are given by:

`df = n_A +n_B -2 = 18 +15-2= 31`

And the 90% confidence interval for this case is:

`-1.90 \leq \mu_A -\mu_B \leq 0.13`

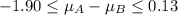
And for this case since the confidence interval contains the value 0 we can conclude that:

A. We are 90% confident that, on average, there is no difference in operating hours between toothbrushes from Company A compared to those from Company B.

Explanation:

We know the following info given:

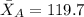`\bar X_A= 119.7` sample mean for A

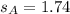`s_A = 1.74` sample deviation for A

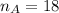`n_A = 18` sample size from A

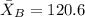`\bar X_B= 120.6` sample mean for B

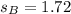`s_B = 1.72` sample deviation for B

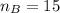`n_B = 15` sample size from B

The degrees of freedom are given by:

`df = n_A +n_B -2 = 18 +15-2= 31`

And the 90% confidence interval for this case is:

`-1.90 \leq \mu_A -\mu_B \leq 0.13`

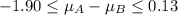
And for this case since the confidence interval contains the value 0 we can conclude that:

A. We are 90% confident that, on average, there is no difference in operating hours between toothbrushes from Company A compared to those from Company B.