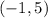Answer:
a)
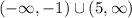
b)
Explanation:
The first step to solve this question is finding the roots of the derivative of x.
Solving a quadratic equation:
Given a second order polynomial expressed by the following equation:
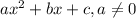 .
.
This polynomial has roots
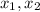 such that
such that
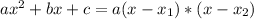 , given by the following formulas:
, given by the following formulas:
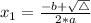
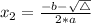

In this question:
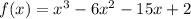
So
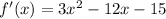
Finding the roots:

Simplifying by -3
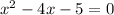
So
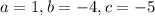
Then



So the function can be divided in three intervals.
They are:
Less than -1
Between -1 and 5
Higher than 5
In which it increases and which it decreases?
Less than -1
Lets find the derivative in a point in this interval, for example, -2
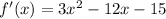
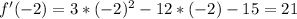
Positive.
So in the interval of
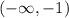 , the function increases.
, the function increases.
Between -1 and 5
Will choose 0.
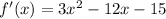
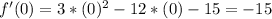
Negative.
So in the interval of
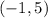 , the function decreases.
, the function decreases.
Higher than 5
Will choose 6.
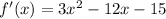
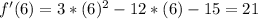
Positive
So in the interval of
 , the function increases.
, the function increases.
(a) Find the interval on which f is increasing.
Using interval notation
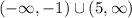
b) Find the interval on which f is decreasing.