Answer:
r = 9.27*10^-4m
Step-by-step explanation:
Given the following parameters;
Tension in the wire T = 821N
wave speed of the transverse wave v = 185m/s
density of nickel = 8.9*10³kg/m³
radius of the wire = ?
Using the relationship for finding the speed of the wave to first get the linear density;
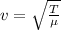 where
where
 is the linear density
is the linear density
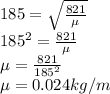
Also;
 = mass m/Length L
= mass m/Length L
Since mass m = density
 * volume
* volume

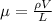
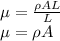
Since A = area of the wire =

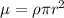
Given

0.024 = 8.9*10³*3.14r²
0.024 = 27.946r²
r² = 0.024/27.964
r² = 8.6*10^-7
r =√8.6*10^-7
r = 9.27*10^-4m
Radius of the wire is 9.27*10^-4m