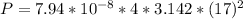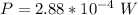Answer:
The power is
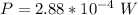
Step-by-step explanation:
From the question we are told that
The distance from the siren is
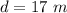
The intensity level is

The threshold of hearing is
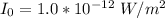
Generally the intensity level is mathematically represented as
![\beta = 10dB * log [(I)/(I_o) ]](https://img.qammunity.org/2021/formulas/physics/college/9ao1v0p30m93pwbpa0x0ez4tjv1gdnp11h.png)
Where I is the intensity at which the siren radiates the sound
substituting values
![49 = 10 * log [(I)/(1.0 *10^(-12)) ]](https://img.qammunity.org/2021/formulas/physics/college/24vd3vfnxf89nx980s9n4p5g21cozyt9vt.png)
=>

Now the amount of power the siren put out is mathematically evaluated as
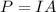
Where A is the area of the siren which is taken as a sphere and it is mathematically evaluated as
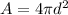
So

substituting values