Answer:
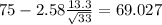
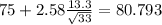
And the 95% confidence interval would be between (69.027;80.793)
Explanation:
Information given
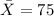 represent the sample mean
represent the sample mean
 population mean (variable of interest)
population mean (variable of interest)
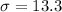 represent the population standard deviation
represent the population standard deviation
n=33 represent the sample size
Confidence interval
The confidence interval for the mean is given by the following formula:
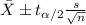 (1)
(1)
The degrees of freedom are given by:
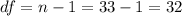
The Confidence level is 0.99 or 99%, the significance would be
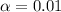 and
and
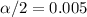 , the critical value for this case would be
, the critical value for this case would be
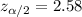
And replacing we got:
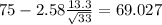
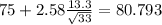
And the 95% confidence interval would be between (69.027;80.793)