Question

The graph represents this system of equations. A system of equations. y equals 4 minus x. y equals y minus 2. A coordinate grid with 2 lines. The first line passes through (0, 4) and (3, 1). The second line passes through (0, negative 2) and (3, 1). What is the solution to the system of equations? (–2, 4) (1, 3) (2, 4) (3, 1)

Answer 1

d (3,1)

Explanation:

Answer 2

(3,1) is the correct answer.

Explanation:

It is given that first line passes through (0,4) and (3,1)

Let the two points be at coordinates:

`(x_1,y_1)` and
`(x_2,y_2)`

`x_1=0,\\y_1= 4,\\x_2=3,\\y_2= 1`

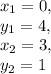
Equation of a line using two coordinates is given as:

`y = mx+c`

`m = (y_2-y_1)/(x_2-x_1) = (1-4)/(3-0) = (-3)/(3) =-1`

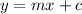
Put x = 0, y = 4

`4 = 0 +c\\\Rightarrow c = 4`

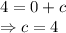
So, first equation is:
`y = -x +4 ...... (1)`

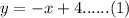
It is given that second line passes through (0,-2) and (3,1)

Let the two points be at coordinates:

`(x_1,y_1)` and
`(x_2,y_2)`

`x_1=0,\\y_1= -2,\\x_2=3,\\y_2= 1`

Equation of a line using two coordinates is given as:

`y = mx+c`

`m = (y_2-y_1)/(x_2-x_1) = (1-(-2))/(3-0) = (3)/(3) =1`

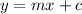
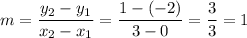
Put x = 0, y = -2

`-2 = 0 +c\\\Rightarrow c = -2`

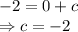
So, second equation is:
`y = x -2 ...... (2)`

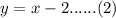
Solving equations (1) and (2) using substitution:

Adding Equation (1) and (2):

`2y = 4-2\\\Rightarrow y =1`

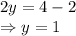
Putting value y = 1 in equation (1):

`1 = -x+4\\\Rightarrow x =3`

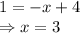
So, the solution for the system of equations is: (3,1)