Answer:
2 and one half
Explanation:
Given
ABC = (4,4),(7,8),(10,4)
A'B'C' = (10,10),(17,20),(25,10)
Required:
Find the Scale Factor
Let the scale factor be represented by s
The relationship between ABC, A'B'C' and s is given as
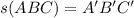
From the given parameters;
A = (4,4) when A' = (10,10)
Using this values;we have

Divide both sides by (4,4)
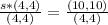

Divide 10 by 4; This gives 2.5
So,
s = 2.5
Using Point B and B'
B = (7,8) when A' = (17,20)
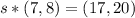
Divide both sides by (7,8)
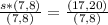

Divide 17 by 7 and 20 by 8; This gives 2.5
So,
s = 2.5
Using Point C and C'
C = (10,4) when C' = (25,10)
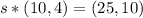
Divide both sides by (10,4)
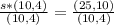
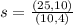
Divide 25 by 10 and 10 by 4; This gives 2.5
So,
s = 2.5
Hence, the scale factor is 2 and one-half(
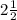 )
)