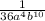Answer : The correct option is
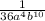
Step-by-step explanation :
According to the BODMAS rule, when the expression contains brackets open ((), {}, []) we have to first simplify the bracket followed by of (powers and roots etc.) and then we have to solve the division, multiplication, addition and subtraction from left to right order (respectively).
The given expression is:
![[((2a^(-3)b^4)^2)/((3a^5b)^(-2))]^(-1)](https://img.qammunity.org/2021/formulas/mathematics/college/amynl1ljizf8kxpcs7e9r5x8wnrowyyufg.png)
![=[((3a^5b)^(-2))/((2a^(-3)b^4)^2)]^(1)](https://img.qammunity.org/2021/formulas/mathematics/college/4fw1cul6spl8duhnnq8tlb6x7r86o0z7ga.png)
![=[(1)/((3a^5b)^(2))* (1)/((2a^(-3)b^4)^2)]](https://img.qammunity.org/2021/formulas/mathematics/college/w60jqbfrirsa0swgr4mvhkxs4jv1cr4pgg.png)
![=[(1)/(9a^(10)b^2)* (1)/(4a^(-6)b^8)]](https://img.qammunity.org/2021/formulas/mathematics/college/m5x4tqmw69f8w321vyipx2eaxza4vzgmdp.png)
![=[(1)/(9a^(10)b^2)* (a^6)/(4b^8)]](https://img.qammunity.org/2021/formulas/mathematics/college/xmqct0jcrk71veo6rvb6nt0532hb42rzlc.png)
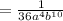
Thus, the given expression is equivalent to