The magnitude of the boat's resultant velocity to the nearest whole number is approximately 31 m/s.
How to find the magnitude of the boat's resultant velocity
To find the magnitude of the boat's resultant velocity, break down the boat's motion into its horizontal and vertical components and then calculate the resultant velocity using vector addition.
First, consider the boat's motion during the first hour, traveling at 15 m/s in a direction 45° east of north.
The horizontal component of velocity (Vx₁) can be found using the cosine function:
Vx₁ = 15 m/s * cos(45°)
The vertical component of velocity (Vy₁) can be found using the sine function:
Vy₁ = 15 m/s * sin(45°)
Next, consider the boat's motion during the second hour, traveling at 18 m/s in a direction 5° north of east.
The horizontal component of velocity (Vx₂) can be found using the cosine function:
Vx₂ = 18 m/s * cos(5°)
The vertical component of velocity (Vy₂) can be found using the sine function:
Vy₂ = 18 m/s * sin(5°)
Now, calculate the total horizontal and vertical velocities:
Total horizontal velocity (Vx) = Vx₁ + Vx₂
Total vertical velocity (Vy) = Vy₁ + Vy₂
To find the magnitude of the resultant velocity (V), use the Pythagorean theorem:
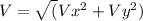
Now, substitute the values and calculate the magnitude of the boat's resultant velocity:
Vx₁ = 15 m/s * cos(45°) ≈ 10.61 m/s
Vy₁ = 15 m/s * sin(45°) ≈ 10.61 m/s
Vx₂ = 18 m/s * cos(5°) ≈ 17.92 m/s
Vy₂ = 18 m/s * sin(5°) ≈ 1.57 m/s
Vx =Vx₁ + Vx₂ ≈ 10.61 m/s + 17.92 m/s ≈ 28.53 m/s
Vy = Vy₁ + Vy₂ ≈ 10.61 m/s + 1.57 m/s ≈ 12.18 m/s
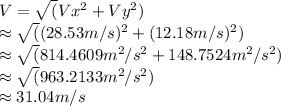
Rounding the magnitude of the boat's resultant velocity to the nearest whole number, we get approximately 31 m/s.