Question

2. Emma is playing a game with two fair dice.

She needs to score 5, using both dice, to win the
game.
What's the probability she will win the game?

Answer 1

The required probability is:

`(1)/(9)`

Explanation:

It is given that Emma has two fair dice.

To win, she needs to score 5 using both dice.

Cases, where she can have 5:

{(1,4), (4,1), (2,3), (3,2)}

Let the event be A that she gets a score = 5

Total number of favorable cases, n(A) = 4

Total number of cases for throw of 2 dice, n(S) = 36

These are:

{

(1,1) (1,2) (1,3) (1,4) (1,5) (1,6)

(2,1) (2,2) (2,3) (2,4) (2,5) (2,6)

(3,1) (3,2) (3,3) (3,4) (3,5) (3,6)

(4,1) (4,2) (4,3) (4,4) (4,5) (4,6)

(5,1) (5,2) (5,3) (5,4) (5,5) (5,6)

(6,1) (6,2) (6,3) (6,4) (6,5) (6,6)

}

Formula for probability of an event E is given as:

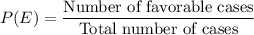
`P(E) = \frac{\text{Number of favorable cases}}{\text {Total number of cases}}`

or

`P(E) = \frac{\text{n(E)}}{\text {n(S)}}`

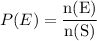
Using the above formula, the required probability:

`P(A) = \frac{\text{n(A)}}{\text {n(S)}}\\\Rightarrow (4)/(36)\\\Rightarrow (1)/(9)`

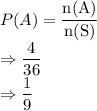
So, the required probability is
`(1)/(9)`.