Question

An enclosed amount of nitrogen gas undergoes thermodynamic processes as follows: from an initial state A to a state B to C to D and back to A, as shown in the P-V diagram. Assume that the gas behaves ideally. What is the change in internal energy of the gas for the entire process, A-B-C-D-A? (pressure at B is 10kPa)

Answer 1

The total internal energy change for the entire process is -0.94 kJ

Step-by-step explanation:

Process A to B is an isothermal process, therefore,
`u_A` -
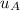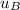`u_B` = 0

Process B to C

P = -mV + C

When P = 12, V = 0.12

When P = 4, V = 0.135

Therefore, we have;

12 = -m·0.12 + C

4 = -m·0.135 + C

Solving gives

m = 533.33

C = 76

`T = (1)/(nR) * (-533.33 * V^2 + 76 * V)`

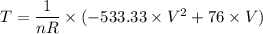
p₂ = p₁V₁/V₂ = 12*0.1/0.12 = 10 kPa

The work done = 0.5*(0.135 - 0.12)*(4 - 10.0) = -0.045 kJ = -45 J

For heat supplied

Assuming an approximate polytropic process, we have;

Work done = (p₃×v₃ - p₂×v₂)/(n - 1)

Which gives;

-45 = (4*0.135 - 10*0.12)/(n -1)

∴ n -1 = (4*0.135 - 10*0.12)/-45 = 14.67

n = 15.67

Q = W×(n - γ)/(γ - 1)

Q = -45*(15.67 - 1.4)/(1.4 - 1) = -1,605.375 J

u₃ - u₂ = Q + W = -1,605.375 J - 45 J = -1650 J = -1.65 kJ

For the constant pressure process D to C, we have;

`Q = c_p * (p)/(R) * (V_4 -V_3) = (5)/(2) * p * (V_4 -V_3)`

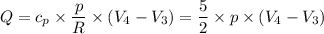
Q₄₋₃ = (0.1 - 0.135) * 4*5/2 = -0.35 kJ

W₄₋₃ = 4*(0.1 - 0.135) = -0.14 kJ

u₄ - u₃ = Q₄₋₃ + W₄₋₃ = -0.14 kJ + -0.35 kJ = -0.49 kJ

For the process D to A, we have a constant volume process

`Q_(1-4) = (c_v)/(R) * V * (p_1 - p_4) = (3)/(2) * 0.1 * (12 - 4) = 1.2 \ kJ`

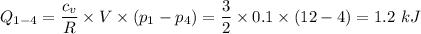
W₁₋₄ = 0 for constant volume process, therefore, u₁ - u₄ = 1.2 kJ

The total internal energy change Δ
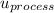`u_(process)` for the entire process is therefore;

Δ
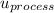`u_(process)` = u₂ - u₁ + u₃ - u₂ + u₄ - u₃ + u₁ - u₄ = 0 - 1.65 - 0.49 + 1.2 = -0.94 kJ.