The car's velocity at time t is given by

It comes to a stop when v = 0, which happens when
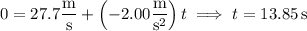
or after about 13.9 s.
In this time, the car travels a distance x given by
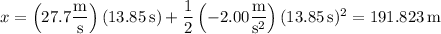
or about 192 m.
In one complete revolution, each tire covers a distance equal to its circumference,

or about 2.14 m.
This means each tire will complete approximately 192/2.14 ≈ 90 revolutions.