Question

A snowball is launched into the air from the top of a parking garage. It's height as a function of time and can be

modeled by the following equations where each equation represents the same scenario:
Standard Form: h(t) = -16^2 + 80t + 300
Vertex Form: h(t) = -16(t - 2.5)² + 400
Factored Form: h(t)= -16(x - 7.5)(x + 2.5)

Answer 1

a. How long after launch did the snowball hit the ground? It took 7.5 time units.

b. How long after the launch did the ball reach its maximum height? The ball reached the maximum height 2.5 time units after its launch.

c. What is the maximum height attained by the snowball? The maximum height achieved by the ball was 400 length units.

d. From what height was the snowball launched? The ball was launched from a height of 300 length units.

Explanation:

The problem gives us three basic forms of the same second degree equation. Each can display one characteristic of the equation more easily than the others. The standard forms quickly tells us what is the height of the snow ball in the start of its movements, in other word the height from the place where it was launched. The vertex form displays the vertex of the movement clearly, in other words it tells us the maximum height and the time it took for the ball to get there. The factored form exposes the roots of the equation, letting us know the time it takes for the ball to hit the ground.

With this in mind lets solve what the problem wants.

a. How long after launch did the snowball hit the ground?

The ground has height equal 0, so we need to find the values of "t" that make the equation have a 0 output. So we want the roots of this equation, these are easily seen on the factored form:

`h(t) = -16*(x - 7.5)*(x + 2.5)`

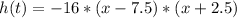
The roots of the equations are 7.5 and - 2.5, because if we use this values for "x" they'll result in a height equal zero. Since there can't be a negative time, the ball took 7.5 s to hit the ground.

b. How long after the launch did the ball reach its maximum height?

c. What is the maximum height attained by the snowball?

The maximum height is the vertex of this equation. The vertex form gives us the coordinates of the vertex, which is (2.5,400), in order words the maximum height is 400 length units and the time it took to get there was 2.5 time units.

d. From what height was the snowball launched?

This can be easily seen from the standard form, since it's the number which is not multiplied by the independent variable, t. In this case the ball was launched from 300 length units.