Question

A person must score in the upper of the population on an IQ test to qualify for membership in Mensa, the international high-IQ society. There are Mensa members in countries throughout the world (Mensa International website, January , ).If IQ scores are normally distributed with a mean of and a standard deviation of , what score must a person have to qualify for Mensa (to whole number)

Answer 1

A person must have a score of at least 131(using the parameters I used).

Explanation:

When the distribution is normal, we use the z-score formula.

In a set with mean
`\mu` and standard deviation
`\sigma`, the zscore of a measure X is given by:

`Z = (X - \mu)/(\sigma)`

The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the pvalue, we get the probability that the value of the measure is greater than X.

In this question:

There was a small typing mistake, and the mean and the standard deviation were not given. Typically, in IQ problems,
`\mu = 100, \sigma = 15`

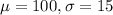
What score must a person have to qualify for Mensa?

I will say that a person must be in the top 2%.

So the score is the 100-2 = 98th percentile, which is X when Z has a pvalue of 0.98. So X when Z = 2.054.

`Z = (X - \mu)/(\sigma)`

`2.054 = (X - 100)/(15)`

`X - 100 = 15*2.054`

`X = 130.81`

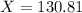
Rounding to the nearest whole number.

A person must have a score of at least 131(using the parameters I used).