Question

An application of the sampling distribution of a proportion

Of the 21.4 million U.S. firms without paid employees, 32% are female owned. [Data source: U.S. Census Bureau; data based on the 2007 Economic Census.]


A simple random sample of 503 firms is selected. Use the Distributions tool to help you answer the questions that follow.


Normal Distribution


Mean = 0.22


Standard Deviation = 0.025


The probability that the sample proportion is within ±.01 of the population proportion is ________.


Suppose the sample size is increased to 903. The probability that the sample proportion is within ±.01 of the population proportion is now ________.

Answer 1

(1) 0.3108

(2) 0.5223

Explanation:

The information provided is:

Mean = p = 0.22

Standard Deviation = 0.025

n = 503

Compute the probability that the sample proportion is within ±0.01 of the population proportion as follows:

`P(-0.01<\hat p-p<0.01)=P((-0.01)/(0.025)<(\hat p-p)/(\sigma_(p))<(-0.01)/(0.025)})`

`=P(-0.40<Z<0.40)\\\\=P(Z<0.40)-P(Z<-0.40)\\\\=0.65542-0.34458\\\\=0.31084\\\\\approx 0.3108`

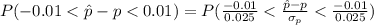
*Use a z-table.

Thus, the probability that the sample proportion is within ±0.01 of the population proportion is 0.3108.

The new sample size is, n = 903.

Compute the standard deviation as follows:

`\sigma_(p)=\sqrt{\farc{p(1-p)}{n}}=\sqrt{(0.22(1-0.22))/(903)}=0.014`

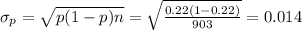
Compute the probability that the sample proportion is within ±.01 of the population proportion as follows:

`P(-0.01<\hat p-p<0.01)=P((-0.01)/(0.014)<(\hat p-p)/(\sigma_(p))<(-0.01)/(0.014)})`

`=P(-0.71<Z<0.71)\\\\=P(Z<0.71)-P(Z<-0.71)\\\\=0.76115-0.23885\\\\=0.5223`

Thus, the probability that the sample proportion is within ±.01 of the population proportion is 0.5223.