Answer:
a) 0.076
b) 0.5
c) 0.084
d) 0.25
e) 0.00024
f) 0.156
Explanation:
a) In an ordinary deck there are 4 aces. The probability of getting an ace is given by:
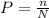
n: options for an ace = 4
N: total number of cards = 52
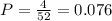
The probability is 7.6%
b) On the first 100 positive integers, there are 50 odd integer numbers. Then you have:
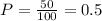
The probability of getting an odd number is 50%
c) From a total of 365 day in the year, May has 31 day. Then you have:

The probability is 8.4%
d) In this case you have two events. To get an odd number with the sum of the number of two dices you need and odd number in one dice and a pair number in the other dice.
The probability is the product of the occurrence of both events. The probability for an odd number is 1/2 and for a pair number is 1/2.
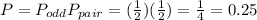
The probability is 25%
e) To obtain Head 6 times in a row, the probability is:
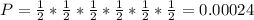
Probability of 0.024%
f) To get Head 4 times from 5 flights, you first calculate the probability for 1 head in five flips:
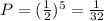
There are 5 forms of getting 4 Heads for 5 flips, then you have:

Te probability is 15.6%