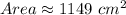Answer:
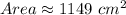
Explanation:
Given that:
ΔUVW,
Side w = 44 cm, (It is the side opposite to
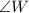 )
)
Side u = 83 cm (It is the side opposite to
 )
)
and ∠V=141°
Please refer to the attached image with labeling of the triangle with the dimensions given.
Area of a triangle with two sides given and angle between the two sides can be formulated as:
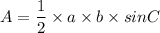
Where a and b are the two sides and
 is the angle between the sides a and b
is the angle between the sides a and b
Here we have a = w = 44cm
b = u = 44cm
and ∠C= ∠V=141
Putting the values to find the area:
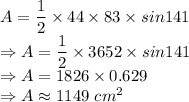
So, the area of given triangle to the nearest square centimetre is: