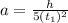Question

A person is standing on an elevator initially at rest at the first floor of a high building. The elevator then begins to ascend to the sixth floor, which is a known distance h above the starting point. The elevator undergoes an unknown constant acceleration of magnitude a for a given time interval T. Then the elevator moves at a constant velocity for a time interval 4T. Finally the elevator brakes with an acceleration of magnitude a, (the same magnitude as the initial acceleration), for a time interval T until stopping at the sixth floor.

Answer 1

The found acceleration in terms of h and t is:

`a=(h)/(5(t_1)^2)`

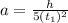
Step-by-step explanation:

(The complete question is given in the attached picture. We need to find the acceleration in terms of h and t in this question)

We are given 3 stages of movement of elevator. We'll first model them each of the stage one by one to find the height covered in each stage. After that we'll find the total height covered by adding heights covered in each stage, and equate it to Total height h. From that we can find the formula for acceleration.

Stage 1

Constant acceleration, starts from rest.

Distance =
`y = (1)/(2)a(t_1)^2`

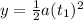
Velocity =
`v_1=at_1`

Stage 2

Constant velocity where

Velocity =
`v_o=v_1=at_1`

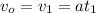
Distance =

`y_2=v_2(t_2)\\\text{Where~}t_2=4t_1 ~\text{and}~ v_2=v_1=at_1\\y_2=(at_1)(4t_1)\\y_2=4a(t_1)^2\\`

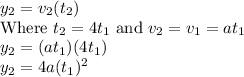
Stage 3

Constant deceleration where

Velocity =
`v_0=v_1=at_1`

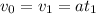
Distance =

`y_3=v_1t_3-(1)/(2)a(t_3)^2\\\text{Where}~t_3=t_1\\y_3=v_1t_1-(1)/(2)a(t_1)^2\\\text{Where}~ v_1t_1=a(t_1)^2\\y_3=a(t_1)^2-(1)/(2)a(t_1)^2\\\text{Subtracting both terms:}\\y_3=(1)/(2)a(t_1)^2`

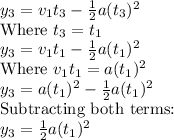
Total Height

Total height = y₁ + y₂ + y₃

Total height =
`(1)/(2)a(t_1)^2+4a(t_1)^2+(1)/(2)a(t_1)^2 = 5a(t_1)^2`

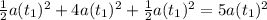
Acceleration

Find acceleration by rearranging the found equation of total height.

Total Height = h

h = 5a(t₁)²

`a=(h)/(5(t_1)^2)`