Question

A survey of 80 homes in a Washington D.C. suburb showed that 45 were air conditioned. A sample of 120 homes in a Pittsburgh suburb showed tht 63 had air conditioning. At α = 0.05, is there a difference in the two proportions? Please show all 4 steps of the classical approach clearly.

Answer 1

There is no significant difference between the two proportions

Explanation:

State the hypotheses:

Null hypothesis -> H0: P1 = P2

Alternative hypothesis -> H1: P1 not = P2

Note that hypotheses constitute a two-tailed test. the null hypothesis will be rejected if the proportion from population 1 is too big or if it is too small.

Formulate an analysis plan

For the analysis, the significance level is 0.05. The test method is a two-proportion z-test.

Analyze sample data.

Using sample data we calculate the pooled sample porportion (p) and the standard error (SE). Using those measures, we compute the z-score test statistic (z).

p = (p1*n1 + p2*n2)/(n1 + n2)

p1 = 45/80 = 0.5625

p2 = 63/120 = 0.525

n1 = 80

n2 = 120

p = (0.5625*80 + 0.525*120)/(80 + 120)

p = 0.54

`SE = \sqrt{p*(1-p)*((1)/(n_(1) ) +(1)/(n_(2)) )}`

`SE = √((0.2428)*(0.0125 + 0.0083))`

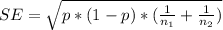
SE = 0.07112

z = (p1 - p2)/ SE

z = (0.5625 - 0.525)/0.07112

z = 0.527

For z = 0.527 we have p-value 0.198

Interpret results. Since p - Value (0.198) of the test is greater than the alpha-0.05 (For two tailed test α-0.025). Therefore we cannot reject the null hypothesis.

There is no significant difference between the two proportions