Question

Grade A sugar costs £75 per kg and grade B sugar costs £50 per kg. Anne mixed the two grades and sold the mixture at £72 per kg. I'm doing so she made a 20% profit. In what ratio did she mix them?​

Answer 1

The ratios must be 88% of grade A sugar and 12% of grade B sugar.

Explanation:

On the grade A every kg costs £75, while on the grade B every kg costs £50. The final mixture we want to make needs to cost £72 per kg. We will sum a certain mass of grade A, "x", with a certain mass of grade B, "y". The sum of these masses must be equal to 1 kg. So we have:

`x + y = 1`

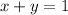
Since we want the final mixture to cost £72, we need to satisfy:

`75*x+ 50*y = 72`

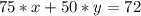
Solving the system of equation will reveal the ration that must be used.

`\left \{ {{x + y=1} \atop {75*x + 50*y=72}} \right.\\ \left \{ {{-50*x + -50*y=-50} \atop {75*x + 50*y=72}} \right.\\25*x = 22\\x = (22)/(25) = 0.88\\y + x = 1\\y = 1 - x \\y = 1 - 0.88 = 0.12`

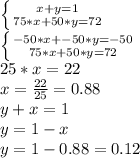
The ratios must be 88% of grade A sugar and 12% of grade B sugar.