Question

IM Systems assembles microcomputers from generic components. It purchases flat screen monitors from a manufacturer in Taiwan; thus, there is a long lead time of 25 days. Daily demand is normally distributed with a mean of 3.5 monitors and a standard deviation of 1.2 monitors. The company maintains a 90% customer service level. How much safety stock of monitors should IM Systems hold

Answer 1

Given Information:

Mean daily demand = 3.5 monitors

standard deviation daily demand = 1.2 monitors

Lead time = 25 days

customer service level = 90%

Required Information:

Safety Stock = ?

Answer:

Safety Stock = 8 monitors

Explanation:

The safety stock of monitors that IM Systems should hold is given by

`Safety \:\: Stock = z * \sigma * √(n)`

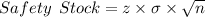
Where σ is the standard deviation of daily demand, n is the lead time and z is the z-score corresponding to 90% service level.

From the z-table, the z-score corresponding to 90% is found to be

z = 1.282

So the required safety stock is

`Safety \:\: Stock = z * \sigma * √(n) \\\\Safety \:\: Stock = 1.282 * 1.2 * √(25) \\\\Safety \:\: Stock = 1.282 * 1.2 * 5 \\\\Safety \:\: Stock = 7.692\\\\`

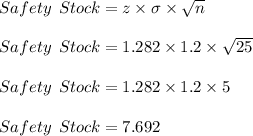
Rounding off to nearest whole number yields

Safety Stock = 8 monitors

Therefore, IM Systems should hold 8 monitors.