Question

A professional employee in a large corporation receives an average of μ = 39.8 e-mails per day. Most of these e-mails are from other employees in the company. Because of the large number of e-mails, employees find themselves distracted and are unable to concentrate when they return to their tasks. In an effort to reduce distraction caused by such interruptions, one company established a priority list that all employees were to use before sending an e-mail. One month after the new priority list was put into place, a random sample of 38 employees showed that they were receiving an average of x = 33.1 e-mails per day. The computer server through which the e-mails are routed showed that σ = 16.2. Has the new policy had any effect? Use a 10% level of significance to test the claim that there has been a change (either way) in the average number of e-mails received per day per employee.

Answer 1

Explanation:

Hello!

The variable of interest is

X: number of emails a profession employee receives per day

This variable has an average of μ= 39.8 emails/day and the standard deviation is known to be δ= 16.2 emails/day

A company considers that the large amount of emails creates distraction, reducing the employees concentration and thus their efficiency, so they established a new priority list that all employees were to use before sending an e-mail. After one month they took a random sample of employees obtaining:

n= 38

X[bar]= 33.1 emails/day

If the company's new policy worked, then the company would expect the mean number of emails an employee receives per day to decrease, symbolically: μ < 39.8

The hypotheses are:

H₀: μ ≥ 39.8

H₁: μ < 39.8

α: 0.10

To analyze the population mean you need as condition that the variable of interest is at least normal.

There is no information about the population distribution, but the sample size is big enough for it to be valid to apply the Central Limit Theorem. This states that for variables of unknown distribution, if a sample large enough is taken (normally n≥30 is considered ok) you can approximate the distribution of the sample mean to normal:

X[bar]≈N(μ;σ²/n)

This allows you to use the standard normal as statistic for the test:

Z= (X[bar] - μ)/(σ/n) ≈ N(0;1)

`Z_(H_0)= (33.1-39.8)/((16.2)/(√(38) ) )= -2.549= -2.55`

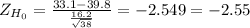
Using the critical value approach, this test is one tailed to the left, meaning that you will reject the null hypothesis to low values of Z.

The critical value is:

`Z_(\alpha )= Z_(0.10)= -1.283`

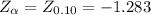
The decision rule is:

If
`Z_(H_0)` ≤ -1.283, reject the null hypothesis.

If
`Z_(H_0)` > -1.283, do not reject the null hypothesis.

The calculated value is less than the critical value so the decision is to reject the null hypothesis.

At a 10% significance level, the null hypothesis was rejected. You can conclude that the new policy reduced the average number of emails a professional employee receives per day.

I hope this helps!

Answer 2

The policy has an effect because the null hypothesis rejected since P-value < significance level.

Explanation:

Since (P-value = 0.0108) < 0.1 significance level, we have sufficient evidence to show that the mean is not equal to 39.8. This means that the policy has an effect on the average number of the emails received per day.

The workings are clearly written in the file attached below. Please check.