Answer: The nth term is
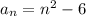
n is any positive integer (1,2,3,...)
===================================================
Work Shown:
The jump from -5 to -2 is +3
The jump from -2 to 3 is +5
The jump from 3 to 10 is +7
The jump from 10 to 19 is +9
Focusing on the increases we see: 3, 5, 7, 9
This is an arithmetic sequence of its own. It steadily increases by 2 each time. Because of this, we can say that the original sequence is a quadratic one.
It is of the form an^2 + bn + c
-----------
Plug in n = 1 to get
an^2 + bn + c = a(1)^2 + b(1) + c = a+b+c
This is set equal to -5 as this is the first term; meaning we have a+b+c = -5
-----------
Now plug in n = 2
an^2 + bn + c = a(2)^2 + b(2) + c = 4a+2b+c
Set this equal to -2, as this is the second term, getting 4a+2b+c = -2
-----------
Plug in n = 3 and follow the same basic steps as before
an^2 + bn + c = a(3)^2 + b(3) + c = 9a+3b+c
We get 9a+3b+c = 3 due to 3 being the third term
-----------
The system of equations we end up with are
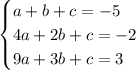
Solve this system however you like. One option is to use a matrix (either inverse or RREF), or you could use elimination. Graphing is not really feasible here. Whichever method you pick, you should end up with the solution (a,b,c) = (1,0,-6)
Meaning, a = 1, b = 0, c = -6
Therefore, an^2 + bn + c would update to 1n^2+0n+(-6) which is the same as n^2 - 6 which is the nth term we're after
-----------
As a check, plug in n = 1 and see what happens. We should get -5 as a result
n^2 - 6 = 1^2 - 6 = -5
Checks out. Let's try n = 2
n^2 - 6 = 2^2 - 6 = -2
That works as well. I'll let you check the others.