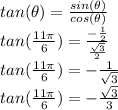Question

4
What is tan 11pi/6​

Answer 1

`tan((11\pi)/(6)) =-(√(3) )/(3)`

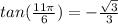
Explanation:

Notice that
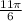`(11\pi)/(6)` is an angle in the fourth quadrant (where the tangent is negative), and the angle is in fact equivalent to
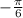`-(\pi)/(6)`. This is one of the special angles for which the sine and cosine functions, as well as the tangent function have well know values:

Recall that the tangent is defined as

`tan(\theta)=(sin(\theta))/(cos(\theta))`

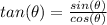
and for this angle (
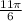`(11\pi)/(6)` ) the value of the sine and cosine functions are well known:

`sin ((11\pi)/(6)) =-(1)/(2) \\cos( (11\pi)/(6)) =(√(3) )/(2)`

Then, the tangent would be:

`tan(\theta)=(sin(\theta))/(cos(\theta))\\tan((11\pi)/(6)) = (-(1)/(2) )/((√(3) )/(2) ) \\tan((11\pi)/(6)) =-(1)/(√(3) ) \\tan((11\pi)/(6)) =-(√(3) )/(3)`