Question

The area of a triangle is 20 cm², and the

altitude is 4 cm greater than the base. Find
the length of the base, to the nearest
millimetre

Answer 1

Heavenly, we need the forumula for the area of a triangle, do you know it?

Explanation:

Area of a triangle is (1/2 ) * B*H

where B = base

H = height

then

A = 1/2* B * H

A is given to be 20

B = b

H = b+4

plug all those into the formula,

20 = (1/2)*b*(b+4)

use your algebra skillz :P

20 = 1/2 *(
`b^(2)` + 4b)

20*2 =
`b^(2)` + 4b

40 =
`b^(2)` + 4b

0 =
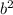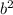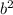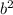`b^(2)` + 4b-40

rewrite the above so it's in x format

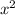`x^(2)` + 4x -40 = 0

use the quadratic formula to find x , and for our problem, remember that x represents the base, or b, but don't mix it up with the b in the quadatic fomula, with the b of the triangle, which is the base, they are differnt "b"s :P

X = (b±
`\sqrt{b^(2)-4*a*c }` ) / 2*a

a = 1

b = 4

c = -40

x = (4±
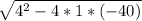`\sqrt{4^(2)-4*1*(-40) }` ) /2*1

x = ( 4±
`√(16+160)` ) / 2

x = (4±
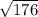`√(176)` ) / 2

x = (4±13.266499)/2

x= 2±6.633249

x = 2 + 6.633249 = 8.633

b= 8.633 cm