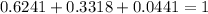Answer:
P = 0.79.
Step-by-step explanation:
To solve this, we need to understand the Hardy-Weinburg equation and what each variable is. P is usually used for the dominant trait classification (in this case, it would be long legs) and Q is usually used for the recessive trait classification (in this case, it would be short legs).
Therefore, we know that the values have to add up to 1 and that Q is recessive and P is dominant. So, if we begin applications, we can learn that to equal 1, we must use numbers less than 1 to accomplish this.
If 21 of a 100-person population have short legs, then ideally, 79 people would have long legs (the dominant trait). So, we know that 0.21 as q and 0.79 as p would equal 1 if you just added p and q together. Therefore, we can know that q is 0.21 and p is 0.79.
To prove this, we can insert these values into the equation: