Answer:
The longer diagonal has a length of 7.3 meters.
The angles are 31.65° and 18.35°
Explanation:
If one angle of the parallelogram is 50°, another angle is also 50° and the other two angles are the supplement of this angle. so the other three angles are:
50°, 130° and 130°.
The longer diagonal will be the one opposite to the bigger angle (130°), and this diagonal divides the parallelogram in two triangles.
Using the law of cosines in one of these two triangles, we have:
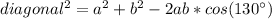

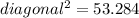
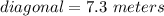
So the longer diagonal has a length of 7.3 meters.
To find the angles that this diagonal forms with the sides, we can use the law of sines:
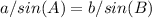
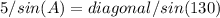
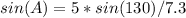
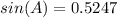
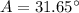
The other angle is B = 50 - 31.65 = 18.35°
Please check the image attached for better comprehension.