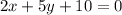Answer: 2x+5y+10=0
Explanation:
The equation of the given line :
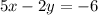 which can be written as
which can be written as
 or
or
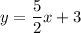 . (i)
. (i)
Linear equation :
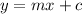 , where m= slope and c = intercept.
, where m= slope and c = intercept.
Comparing this to (i), we get
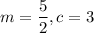
Let
 be the slope of the line perpendicular to the line 5x - 2y = -6 and passes through the point (5,-4).
be the slope of the line perpendicular to the line 5x - 2y = -6 and passes through the point (5,-4).
Since, the product of slopes of two perpendicular lines is -1.
So,
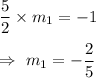
Equation of line passes through (a,b) and have slope n is given by :-
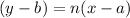
So, Equation of line passes through (5,-4) and have slope
 would be
would be

Required equation :