Question

Pls solve fast!! 65 POINTS worth!! thanks :)

9. Solve the equation log(x+7)-log3=3

a- 3.5
b-142.7
c- 0.0070
d- 0.0707

10. What is the percent rate of change in function y=(0.96)x? Determine whether the function represents exponential growth or exponential decay.

a- 4% exponential decay
b- 4% exponential growth
c- 0.4% exponential growth
d- 0.04% exponential decay

11. Use natural logarithms to solve the equation. Round to the nearest thousandth.
•3e^2x+2=28

a- 1.0797
b- 0.4689
c- 0.9261
d- 2.1595

12. Write the expression as a single logarithm.
•5logby+6logbx

a- logb(yx^5+6)
b- (5+6) logb (y+x)
c- logb(y^5+x^6)
d- logb(y^5x^6)

Answer 1

Step-by-step explanations for each question (question titles in bold):

Question 9:

None of the given values match a value for the equation, so I cannot give an explanation because I am lost as well.

Question 10:

Percent rate of change is the determination by how much of a percent does something exponentially change throughout a given period of time. It will either grow or decay.

Numbers that are within the range of 0.01 to 0.99 will decay, and any number above that defined range will grow. Because 0.96 is between the defined range, this is a decay function. Therefore, we can eliminate options B and C.

Now, because we know that is is decay, we can figure out the depth of the decay. To do this, simply subtract the number in parentheses from 1 (this only works IF and ONLY IF there is a decay!) and determine your percent of decay. Therefore, the final answer is D - 0.04% exponential decay.

Question 11:

Natural logarithms are the ln button on your calculator and use e also. e =
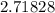`2.71828` where the last 4 digits constantly repeat with no termination. However, for this equation, we do not substitute this value or it will mess up your answer and put you off by a little bit (you will get VERY close to the actual answer, but if it were a fill-in response, your rounding would be off by a couple of digits).

To solve this equation, first subtract 2 from both sides to leave the
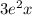`3e^(2)x` lonesome and turn the 28 into 26. This gives us
`3e^(2)x=26`.

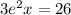Then, divide by the coefficient of 3 on both sides to get
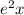`e^(2)x` by itself. This gives us
`e^(2)x = 8.66667`.

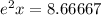Then, we take the natural logarithm of both sides. This cancels out our e and gives us
`2x` on the left and
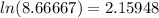`ln(8.66667) = 2.15948`. This leaves us with
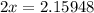`2x = 2.15948` and therefore leaving us with a simple one-step equation remaining.

Finally, just divide both sides by 2 to isolate the x and attach the x to a defined value:
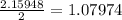`(2.15948)/(2) =1.07974`. Therefore, we can determine that the final answer is A - 1.0797.

Question 12:

The given equation can be written as
`log_(b) (y^(5) +x^(6) )`.

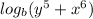To determine this, we can write our given equation as
`5log_(b)y + 6log_(b)x`. Now, we can rearrange this using logarithmic identities (we will be using
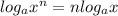`log_(a)x^(n) =nlog_(a)x`). We simply arrange our terms to gain this answer.

Therefore, we just use arrangements to see the given equation in form of the new identity, which rearranging gives us
`log_(b)y^(5) + log_(b)x^(6)`.

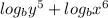Now, we can condense our logarithm because we have the same coefficients and the same bases (identity =
`log_(b)xy = log_(b)x + log_(b)y`).

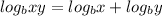So, by breaking up our logarithm and then condensing it, we get
`log_(b)(y^(5)+x^(6))`.

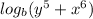Therefore, our final answer is
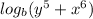`log_(b)(y^(5)+x^(6))`, or answer choice C.