Answer:
a) 109.76 J
b) 3.07 kg-m^2
c) no!
it is not possible to build a wheel with moment of inertia of 10 kg-m^2, with the same mass and radius of the wheel.
Step-by-step explanation:
Radius of the wheel = 0.32 m
mass of the wheel = 30 kg
hanged block mass = 7 kg
height of fall of mass = 2.5 m
final velocity of travel v = 5.6 m/s
initial velocity u = 0 (body is released from rest)
a) According to the energy conservation principle, the kinetic energy of the falling mass will be transformed into the rotational kinetic energy of the wheel
kinetic energy of the falling body =
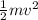
=
 x 7 x
x 7 x
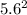 = 109.76 J
= 109.76 J
b) moment of inertia I of the wheel =
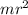
m is mass of the wheel,
r is the radius of the wheel
I = 30 x
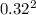 = 3.07 kg-m^2
= 3.07 kg-m^2
c) no!
it is not possible to build a wheel with moment of inertia of 10 kg-m^2, with the same mass and radius of the wheel