Question

A 10-mm steel drill rod was heat-treated and ground. The measured hardness was found to be 290 Brinell. Estimate the endurance strength, Se, in MPa if the rod is used in rotating bending.

Answer 1

the endurance strength
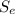`S_e` = 421.24 MPa

Step-by-step explanation:

From the given information; The objective is to estimate the endurance strength, Se, in MPa .

To do that; let's for see the expression that shows the relationship between the ultimate tensile strength and Brinell hardness number .

It is expressed as:

`200 \leq H_B \leq 450`

`S_(ut) = 3.41 H_B`

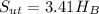
where;

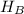`H_B` = Brinell hardness number

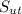`S_(ut)` = Ultimate tensile strength

From ;

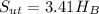`S_(ut) = 3.41 H_B`; replace 290 for
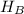`H_B` ; we have

`S_(ut) = 3.41 (290)`

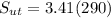
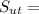`S_(ut) =` 988.9 MPa

We can see that the derived value for the ultimate tensile strength when the Brinell harness number = 290 is less than 1400 MPa ( i.e it is 988.9 MPa)

So; we can say

`S_(ut) < 1400`

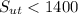
The Endurance limit can be represented by the formula:

`S_e ' = 0.5 S_(ut)`

`S_e ' = 0.5 (988.9)`

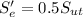
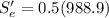
`S_e '` = 494.45 MPa

Using Table 6.2 for parameter for Marin Surface modification factor. The value for a and b are derived; which are :

a = 1.58

b = -0.085

The value of the surface factor can be calculate by using the equation

`k_a = aS^b_(ut)`

`K_a = 1.58 (988.9)^{-0.085`

`K_a = 0.8792`

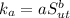
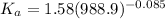
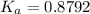
The formula that is used to determine the value of
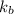`k_b` for the rotating shaft of size factor d = 10 mm is as follows:

`k_b = 1.24d^(-0.107)`

`k_b = 1.24(10)^(-0.107)`

`k_b = 0.969`

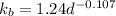
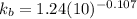
Finally; the the endurance strength, Se, in MPa if the rod is used in rotating bending is determined by using the expression;

`S_e =k_ak_b S' _e`

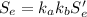
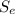`S_e`= 0.8792×0.969×494.45

`S_e` = 421.24 MPa

Thus; the endurance strength
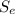`S_e` = 421.24 MPa