Question

J.J.Bean sells a wide variety of outdoor equipment and clothing. The company sells both through mail order and via the internet. Random samples of sales receipts were studied for mail-order sales and internet sales, with the total purchase being recorded for each sale. A random sample of 16 sales receipts for mail-order sales results in a mean sale amount of $74.50 with a standard deviation of $17.25. A random sample of 9 sales receipts for internet sales results in a mean sale amount of $84.40 with a standard deviation of $21.25. Using this data, find the 99% confidence interval for the true mean difference between the mean amount of mail-order purchases and the mean amount of internet purchases. Assume that the population variances are not equal and that the two populations are normally distributed. Step 2 of 3 : Find the margin of error to be used in constructing the confidence interval. Round your answer to six decimal places.

Answer 1

99% confidence interval for the true mean difference between the mean amount of mail-order purchases and the mean amount of internet purchases is [$(-31.82) , $12.02].

Explanation:

We are given that a random sample of 16 sales receipts for mail-order sales results in a mean sale amount of $74.50 with a standard deviation of $17.25.

A random sample of 9 sales receipts for internet sales results in a mean sale amount of $84.40 with a standard deviation of $21.25.

The pivotal quantity that will be used for constructing 99% confidence interval for true mean difference is given by;

P.Q. =
`\frac{(\bar X_1-\bar X_2)-(\mu_1-\mu_2)}{s_p * \sqrt{(1)/(n_1)+(1)/(n_2) } }` ~
`t__n_1_+_n_2_-_2`

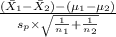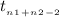
where,
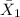`\bar X_1` = sample mean for mail-order sales = $74.50

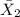`\bar X_2` = sample mean for internet sales = $84.40

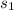`s_1` = sample standard deviation for mail-order purchases = $17.25

`s_2` = sample standard deviation for internet purchases = $21.25

`n_1` = sample of sales receipts for mail-order purchases = 16

`n_2` = sample of sales receipts for internet purchases = 9

Also,
`s_p =\sqrt{((n_1-1)* s_1^(2)+(n_2-1)* s_2^(2) )/(n_1+n_2-2) }` =
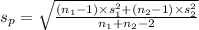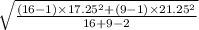`\sqrt{((16-1)* 17.25^(2)+(9-1)* 21.25^(2) )/(16+9-2) }` = 18.74

The true mean difference between the mean amount of mail-order purchases and the mean amount of internet purchases is represented by (
`\mu_1-\mu_2`).

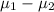Now, 99% confidence interval for (
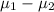`\mu_1-\mu_2`) is given by;

=
`(\bar X_1-\bar X_2) \pm t_(_(\alpha)/(2)_) * s_p * \sqrt{(1)/(n_1) +(1)/(n_2)}`

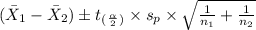
Here, the critical value of t at 0.5% level of significance and 23 degrees of freedom is given as 2.807.

=
`(74.50-84.40) \pm (2.807 * 18.74 * \sqrt{(1)/(16) +(1)/(9)})`

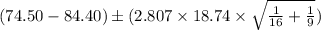
= [$-31.82 , $12.02]

Hence, 99% confidence interval for the true mean difference between the mean amount of mail-order purchases and the mean amount of internet purchases is [$(-31.82) , $12.02].