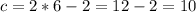Question

For each hour he babysit,Anderson earns 1$ more than half of carey's hourly rate.Anderson earns 6$ per hour. wich equation can be used to solve for carey's hourly rate,c?

Answer 1

A)

6 = c/2 + 1

Answer 2

The expression to find Carey's hourly rate is:
`c = 2*a - 2`. Carey's hourly rate is $10.

Explanation:

Anderson receives 1 more than half of carey's hourly rate. If we call Anderson's rate by "a" and Carey's by "c", we can express this phrase in the following equation:

`a = (c)/(2) + 1`

We want to find the Carey's rate, therefore we need to isolate the "c" variable.

`(c)/(2) + 1 = a\\(c)/(2) = a - 1\\c = 2*a - 2`

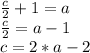
Since Anderson earns $6, then we can find Carey's rate:

`c = 2*6 - 2 = 12 - 2 = 10`