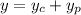Question

The indicated function y1(x) is a solution of the associated homogeneous equation. Use the method of reduction of order to find a second solution y2(x) of the homogeneous equation and a particular solution yp(x) of the given non-homogeneous equation.

y'' − 5y' + 4y = x; y1 = ex
Find yp(x).

Answer 1

The particular integral of given differential equation

`y_(p) = (1)/(4) ( x - ((-5)/(4) ) (1))`

General solution of given differential equation

`y = y_(c) + y_(p)`

`Y (x) = C_(1) e^(x) + C_(2) e^(4x) + (1)/(4) ( x + ((5)/(4) ))`

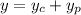
Explanation:

Step(i):-

Given Differential equation y'' − 5 y' + 4 y = x

Given equation in operator form

D²y - 5 Dy + 4 y = x

⇒ ( D² - 5 D + 4 ) y =x

⇒ f(D) y = Q

where f(D) = D² - 5 D + 4 and Q(x) = x

The auxiliary equation f(m) =0

m²-5 m + 4 =0

m² - 4 m - m + 4 =0

m ( m -4 ) -1 ( m-4) =0

(m - 1) =0 and ( m-4) =0

m = 1 and m =4

The complementary function

`Y_(c) = C_(1) e^(x) + C_(2) e^(4x)`

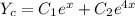
Step(ii):-

particular integral

Particular integral

`y_(p) = (1)/(f(D)) Q(x) = (1)/(D^(2) - 5 D + 4) X`

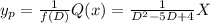
taking common '4'

`= (1)/(4(1 + ((D^(2) - 5 D)/(4) ))) X`

`=(1)/(4) (1 + ((D^(2) -5D)/(4))^(-1) )} X`

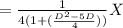
applying binomial expression

( 1 + x )⁻¹ = 1 - x + x² - x³ +.....

`=(1)/(4) (1 - ((D^(2) -5D)/(4)) +(((D^(2) -5D)/(4))^(2) -...} )X`

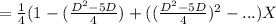
Now simplifying and we will use notation D =
`(dy)/(dx)`

`=(1)/(4) (x - ((D^(2) -5D)/(4))x +(((D^(2) -5D)/(4))^(2)(x) -...}`

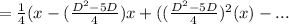
Higher degree terms are neglected

`=(1)/(4) (x - (( -5 D)/(4)) x)`

The particular integral of given differential equation

`y_(p) = (1)/(4) ( x - ((-5)/(4) ) (1))`

Final answer:-

General solution of given differential equation

`y = y_(c) + y_(p)`

`Y (x) = C_(1) e^(x) + C_(2) e^(4x) + (1)/(4) ( x + ((5)/(4) ))`